1D Kinematics¶
Constant Acceleration¶
v_f=v_i+at
x_f=x_i+v_it+\frac{1}{2}at^2
v_f^2-v_i^2=2a(x_f-x_i)
x_f=x_i+v_{avg}t
Centripetal Acceleration¶
a_c=\frac{v^2}{r}=r\omega^2, a_c points to the centre of the circle
Period: T=\frac{2\pi r}{v}
Angular velocity: \omega=\frac{2\pi}{T}=\frac{v}{r} (\omega in rad/s)
Torque¶
| Equation | Explain |
|---|---|
| \tau = rF\sin\theta | r: distance between the point where force is applied and the rotating center F: raw amount of force \theta: angle between F and r |
| \alpha=\frac{\tau}{I} | \alpha: angular acceleration I: moment of inertia / rotational inertia |
| \alpha=\frac{a}{r} | |
| I=mr^2 | moment of inertia of a point mass |
| I=\frac{1}{3}mr^2 | moment of inertia of a rod about its end |
| I=\frac{1}{2}mr^2 | moment of inertia of a circle |
Moment of Inertia¶


Parallel axis¶

Centre of Mass¶

Work¶
| Equation | Explain |
|---|---|
| W=\tau \Delta\theta | |
| P=\tau \omega | |
| K=\frac12 I\omega^2 | K: rotational kinetic energy |
Potential Energy¶
| Equation | Explain |
|---|---|
| U_s=\frac12kx^2 | Elastic Potential Energy |
| U_g=mgh | Gravitational Potential Energy |
Collisions¶
| Equation | Explain |
|---|---|
| p=mv | p: linear momentum (\frac{kg\times m}{s}) |
| I = \Delta p=F\Delta t (for constant force) | \Delta p / I: impulse |
| I\approx\int_{t_i}^{t_f}F_{\text{contact}} | contact inpulse approximation (ignore all other forces) |
| E_k=\frac{p^2}{2m} | |
| \Sigma F = \frac{dp}{dt} | Net external force = rate of change of momentum |
| m_1v_1+m_2v_2=(m_1+m_2)v_f | perfectly inelastic collision (conservation of momentum) |
| v_{1i}-v_{2i}=v_{2f}-v_{1f} | perfectly elastic collision |
| m_1v_{1i}+m_2v_{2i}=m_1v_{1f}+m_2v_{2f} | perfectly elastic collision (conservation of momentum) |
| m_1v_{1i}^2+m_2v_{2i}^2=m_1v_{1f}^2+m_2v_{2f}^2 | perfectly elastic collision (conservation of kinetic energy) |
| v_{1f}=v_{1i}\times\frac{m_1-m_2}{m_1+m_2} v_{2f}=2v_{1i}\times\frac{m_1}{m_1+m_2} |
perfectly elastic collision when v_{2i}=0 |
| Equation | Explain |
|---|---|
| Mv_{CM}=\sum m_iv_i=p_{total} | Total mass x speed of CM = sum of momentum of all particles = momentum of the object |
| \sum(\text{external forces})=M_{total}a_{CM} |
Rolling Motion¶
| Equation | Explain |
|---|---|
| \omega = \frac{v}{R} | \omega: rotating speed |
| \alpha=\frac{a_{CM}}{R} | \alpha: angular acceleration |
| E = \frac12mv^2+\frac12I(\frac{v}{R})^2 | kinetic energy for rolling motion |
Angular Momentum¶
| Equaiton | Explain |
|---|---|
| L=I\omega | L: Angular momentum (\frac{kg\times m^2}{s})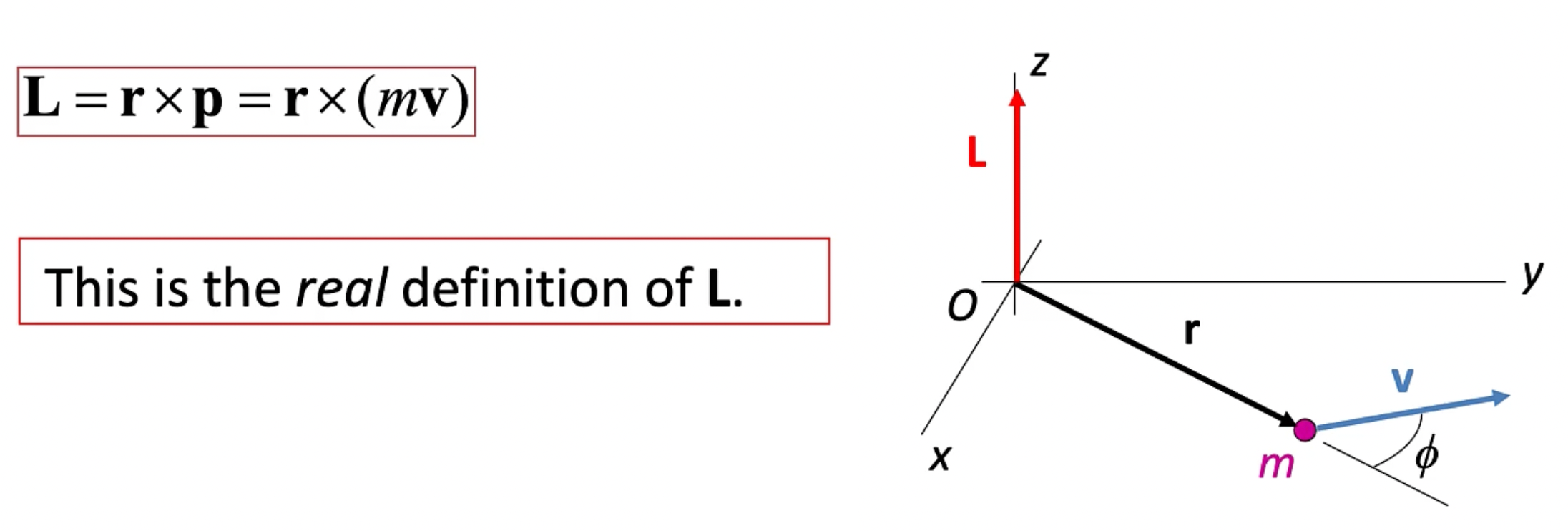 |
| $ | L |
| I_f\omega_f=I_i\omega_i | conservation of angular momentum |
Last update:
December 12, 2021
Created: September 14, 2021
Created: September 14, 2021